Methods and ideas developed in nuclear many-body theory have found useful applications in other fields such as mesoscopic physics and nanoscience. The focus of our research in this area is on small correlated quantum many-body system in which finite-size effects are important, such as nuclei, quantum dots and nano-scale metallic grains. Unlike atomic nuclei, quantum dots are man-made devices and as such their physical parameters can be easily controlled by experimentalists, making them an attractive testing ground of many-body physics.
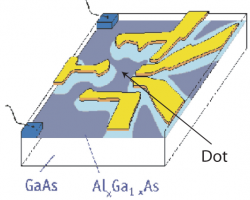 We have made significant contributions at the interface between nuclear physics and mesoscopic physics. In particular, we have developed a theory to quantify the mesosopic fluctuations of the conductance and other observables in almost-isolated quantum dots. This theory is based on random-matrix theory, developed by Wigner and others to explain the statistical fluctuations of the neutron resonances in the compound nucleus. For reviews see RMP 2000 and Nobel Symposium 2001.
We have made significant contributions at the interface between nuclear physics and mesoscopic physics. In particular, we have developed a theory to quantify the mesosopic fluctuations of the conductance and other observables in almost-isolated quantum dots. This theory is based on random-matrix theory, developed by Wigner and others to explain the statistical fluctuations of the neutron resonances in the compound nucleus. For reviews see RMP 2000 and Nobel Symposium 2001.
Our research in this area is focused on the interplay between single-particle mean field degrees of freedom and many-body correlations. The low-energy physics of a mesoscopic structure whose single-particle dynamics are chaotic is described by an effective Hamiltonian known as the universal Hamiltonian. This Hamiltonian includes three interaction terms: charging energy, spin exchange and pairing. In quantum dots the pairing term is repulsive and can be ignored but the exchange interaction term plays an important role. We used spin projection methods, developed in nuclear physics, to calculate the conductance through a weakly coupled dot in closed form, and explained long-standing discrepancies between theory and experiments (PRL 2003). We have also studied the effects of exchange correlations on the thermopower of the dot (PRB 2011).
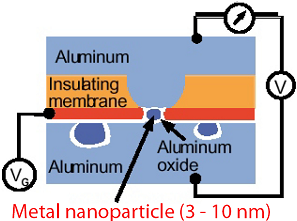 In nano-scale metallic grains, the pairing term is attractive and can lead to a Bardeen-Cooper-Schrieffer (BCS) instability. Of particular interest are grains whose linear size is smaller than a few nanometers. Such grains describe the crossover between the bulk BCS limit and the fluctuation-dominated regime in which BCS theory is no longer valid and the effects of pairing correlations are much more subtle. Anderson argued that this limit corresponds to the smallest size at which a nanoparticle remains a superconductor. The competition between superconductivity (induced by pairing) and ferromagnetism (induced by exchange) in the fluctuation-dominated regime has remarkable signatures in a number of quantities that we have studied: (i) ground-state spin; we identified a coexistence regime of superconductivity and ferromagnetism (EPL 2007), (ii) mesoscopic fluctuations of the conductance peaks in a grain that is weakly coupled to external leads (PRL 2008), and (iii) thermodynamic observables such as the heat capacity and spin susceptibility (PRB 2013). For a review of this work see Phys. Scr. 2012.
In nano-scale metallic grains, the pairing term is attractive and can lead to a Bardeen-Cooper-Schrieffer (BCS) instability. Of particular interest are grains whose linear size is smaller than a few nanometers. Such grains describe the crossover between the bulk BCS limit and the fluctuation-dominated regime in which BCS theory is no longer valid and the effects of pairing correlations are much more subtle. Anderson argued that this limit corresponds to the smallest size at which a nanoparticle remains a superconductor. The competition between superconductivity (induced by pairing) and ferromagnetism (induced by exchange) in the fluctuation-dominated regime has remarkable signatures in a number of quantities that we have studied: (i) ground-state spin; we identified a coexistence regime of superconductivity and ferromagnetism (EPL 2007), (ii) mesoscopic fluctuations of the conductance peaks in a grain that is weakly coupled to external leads (PRL 2008), and (iii) thermodynamic observables such as the heat capacity and spin susceptibility (PRB 2013). For a review of this work see Phys. Scr. 2012.
The fluctuation-dominated regime is common to nanoparticles and nuclei, even though their gaps differ by six orders of magnitude. For a review see the chapter in 50 years of nuclear BCS (2013).
The addition of spin-orbit scattering breaks spin symmetry but preserves time-reversal symmetry. The exchange interaction is then suppressed while the pairing interaction remains unaffected. We have studied the response of discrete energy levels of such a nanoparticle to an external magnetic field (PRB 2015). In particular, we investigated the linear and quadratic terms in the magnetic field that are parametrized by the g-factor and level curvature, respectively. We have found that the g-factor statistics are unaffected by pairing correlations, but the level curvature statistics are very sensitive to pairing and can thus be used to probe pairing correlations in the single-electron tunneling spectroscopy experiments. This probe is particularly useful in the fluctuation-dominated regime, in which the pairing gap cannot be directly observed in the excitation spectrum.
For a recent review of our work on interaction effects in metallic nanoparticles in the absence and presence of spin-orbit scattering, see Progress of Physics 2017.